rhythm/repetition_center/edge

The temporal construct consists of regularly spaced elements whose varying shape illustrates movement. In this animation I attempted to challenge the rhythm/repetition by animating the focal length of the camera. The construct does not move but the focal length starts wide (about 100 degrees) and ends narrow (about 40 degrees) compressing the apparent distance between the parts of the construct in relation to time. By leaving the construct at rest and animating I was attempting to emphasize that the “medium between the observer and the visible object as the reality of visual experience.” (Perez-Gomez)

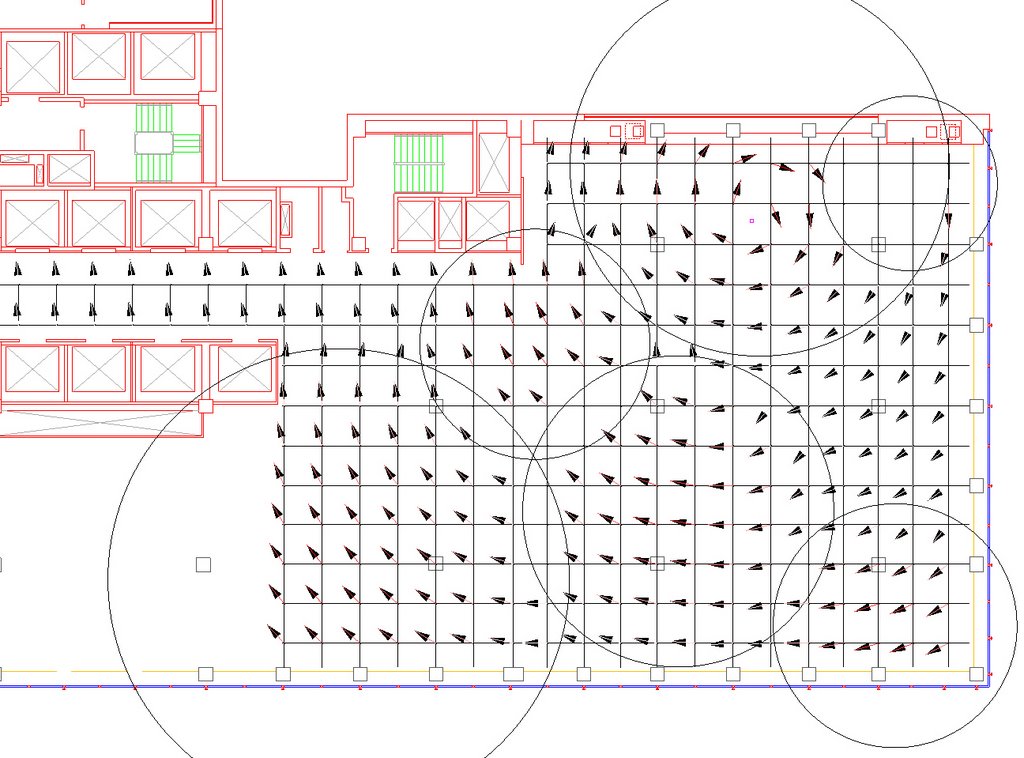
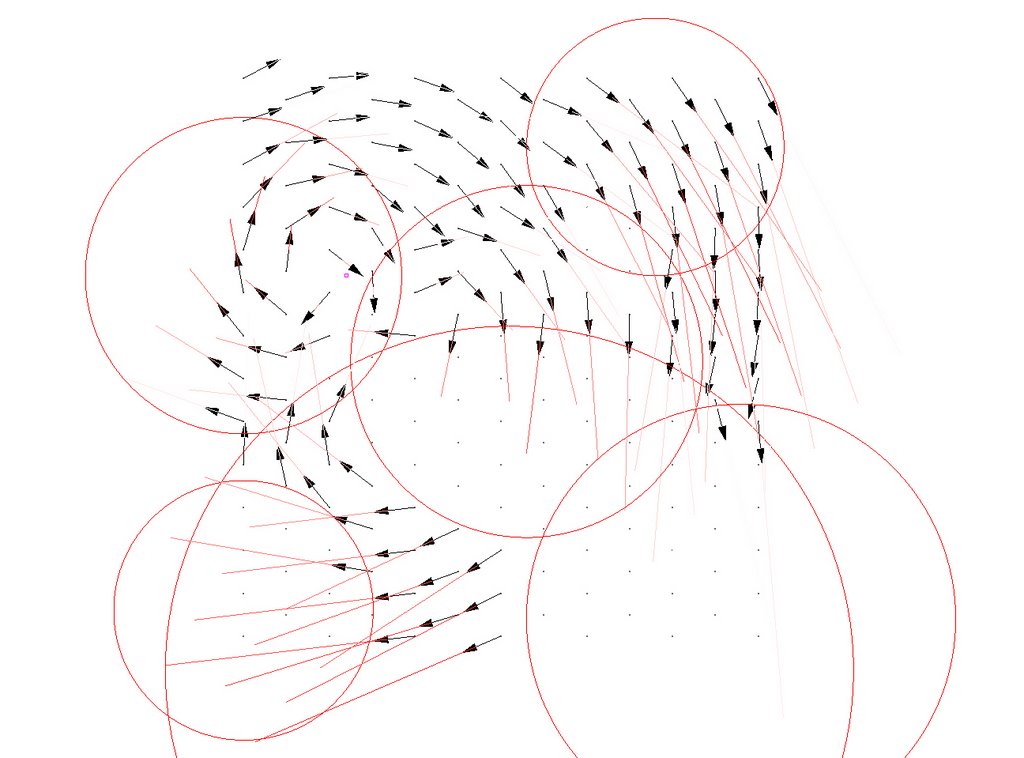
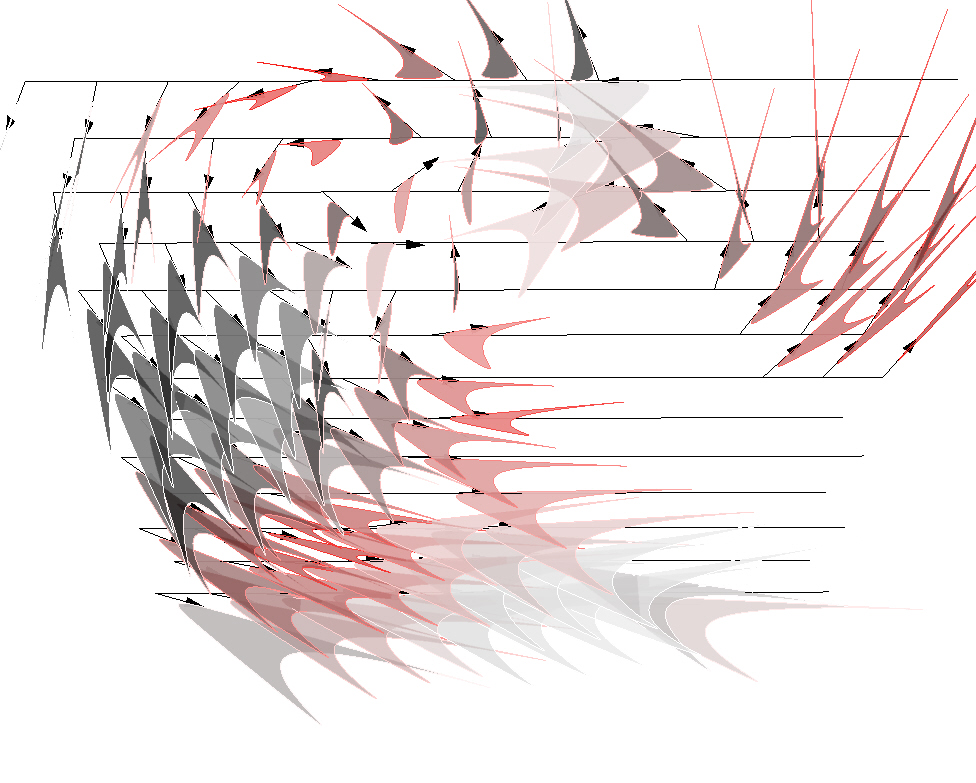
The path and placement of the viewpoint was intended to subvert the reading of frame by putting the center/edge in motion. The viewpoint constantly shifts from one side, to the other side and from inside to outside causing the orientation of the frame to shift similarly.

Alberto Perez-Gomez and a brief history of geometry

Alberto Perez-Gomez and Louise Pelletier, in Architectural Representation and the Perspective Hinge, put in to question architects unwavering faith in the conventional set of projections (plan, section, elevation) that have been used to represent the idea of a building. He points out that they are symbols for a building not the actual building. “For architects it is important to remember that a symbol is neither a contrivance nor an invention—nor is it necessarily a representation of absolute truths or transcendental theological values.” It is clear that the conventional set of architectural projections is neither arbitrary nor a given.

This idea of an (un)stable foundation of conventional architectural representation can be put in relation when compared to the foundations of Euclidean Geometry. In Elements, thirteen books on geometry, Euclid defines an axiomatic system in which a finite set of axioms are take as true (without proof) and all theorems are proved from the initial set of axioms. We cannot prove anything with out accepting something as true or given. Euclid’s five axioms are:
1. Any two points can be joined by a straight line.
2. Any straight line segment can be extended indefinitely in a straight line.
3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
4. All right angles are congruent.
5. Parallel postulate. If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. (essentially, given a line M and a point P not on that line there exists only one line that goes through P and never intersects M.)

He also included 23 definitions such as point, line, and surface in addition to 5 “common notions,” which included, "things which equal the same thing are equal to one another,” and “if equals are added to equals then the sums are equal.” These are concepts that we have to accept as true if we are going to prove anything. Accepting these basic ideas and definitions as true, Euclid proved the theorems that appear in Elements and formed the basis for geometry for the next two thousand years.

Understand Euclidean geometry allows us to deconstruct conventional architectural representation. In architecture we have accepted projection and associated definitions as givens and proved our whole system of representation based on these assumptions. So what happens if we don’t accept the stated axioms as givens? In the early 19th century mathematicians began to question the parallel postulate. Could it be derived in terms of the other four axioms (and hence wasn’t an axiom but a theorem)? Were there theorems that had been derived that didn’t rely on the parallel postulate? It turns out that the first 28 theorems he proved are not derived based on the parallel postulate. This questioning of the fundamental axioms of geometry has led to new geometries. For instance, if we take the parallel postulate as false we get two new axioms, either 'there exists an infinite number of lines through P parallel to M' or 'there exists no lines through P parallel to M.' The former results in hyperbolic geometry and the latter in elliptic geometry.

So what happens if we don’t accept the basic foundation of conventional architectural representation as true? What if we think of them as false? What other systems of representation can be derived?

The most important idea to remember is that treating an underlying principal as false doesn’t necessarily give us the opposite of it. We get systems that are derived from various rule sets. For instance, Gothic architecture “operating though well-established traditions and geometric rules that could be applied directly on site,” was derived from an entirely different system of architectural representation than today. Conversely, contemporary architects are redefining rules within the conventional rule set. This still produces new systems of representation, but ones based on some of the same rules, similar to the Euclidean/Hyperbolic/Elliptic geometry relationship.

Lewis Tsurumaki Lewis has taken the generally accepted rule of ‘conventional architectural representations (plan, section, axon) need to remain separate to convey information’ and negated it, “conventional architectural representations need to be combined (ex. orthographically-projected-plan-sectioned-isometrics) to convey information.’ They have defined a new system based on the traditional conventions of representation and the redefinition of one of those rules. Additionally, SHoP architects have redefined architectural representation based on efficiency resulting in axonometric construction drawings and a general abandonment of orthographically projected architectural representation.

Now we are faced with the challenge of inventing new systems and conventions of architectural representation that are informative and appropriate to contemporary techniques and practices. Do we negate the traditional conventions and start over? Or do we return to older systems, such as the gothic tradition of building? The appropriate approach to rethinking the traditional system of architectural representation is to redefine specific axioms of convention that allow us to construct new systems out the fragments of tradition.

project 1a

relation and orientation

I've introduced a surface that traces the path of each wii mote movement which orients the path and structure of the construct. Here I have represented the paths as red:



I am uncertain if the red is necessary for the paths to be understandable. In the next video they are white. I've also extruded each vector surface to a point to try and map the conceptual center of the motion.




Here are some images investigating the use of red and surface vectors vs extruded mass vectors

Vector Field - The Very Many

In his January 15, 2007 entry The Very Many explores vector fields as an organizing system for the circulation and presentation areas of a gallery. He positions this project in terms of Greg Lynn, "from 'animate' rules, to shift in morphology, to mutate . . . "LE CHAMP"- has been the most litterally expressed via a field vectors, actual device support for presentation panels which should be simply laser-cut onto a full spectrum of colored acrylic panels."

animate wii

The camera is animated along the path of a spline curve generated from the points of the side vector diagram. The focal point of the camera is animated along the path of a spline curve generated from the points of the front vector diagram.

Here is an animation showing the path of the camera and focal point in relation to the construct.

temporal construct

Using the vector diagram of the front view and side view I’ve generated a new 3-demensional abstraction of the wii tennis movement. I rotated the front view vectors 90 degrees and then lofted corresponding vector from each view. This seems like a much better abstraction of wii tennis movement than previous attempts.

informative?

After more attempts at abstracting the wii mote in 3-dimensions I realized that I needed more information for it to be successful. I had only done a vector diagram of the wii mote motion taken from the front view. Here is the vector motion diagram of the side view. Hopefully this will allow me to generate more rigorous and informative 3-dimensional translations.

the hard part

Based on the various attempts at diagramming the motion associated with wii tennis, it’s clear that the vector diagrams of the wii mote force are the most interesting. That said, here is a first attempt at translating the vector wii mote into 3D. I took each vector and swept it along a spline curved generated from the end points of each vector. Interesting but not very informative. It seems like the force associated with each vector gets lost in this abstraction.

Interpreting Motion

Here are spline curves that are normal to the end of the wii mote. Control points are pulled in response to force of motion of each key frame. The top line is from the side view and the bottom line is from the front view. Trends and moments of stasis and motion are clearly evident.

To further respond to issues of force, I next used vectors that represent the force of the wii mote in each key frame.



This made me think of a vector field. This image is the composite overlay of the vectors of each key frame. (It’s not a vector field but resembles one).

Elbow/Wrist/Wii Mote

Here is a translation of the motion of my elbow, wrist, and wii mote into line diagram. The lines in the first image are generated by defining a point of each element (elbow/wrist/wii mote) in each key frame and then connecting them.

Here I've used a color to define the space between each element in the side and front camera views.

Here transitional lines between elbow/wrist/wii mote movement in the side and front views have been introduced. Variation in force are illustrated as well as changes in orientation.


Finally, I have used transitional lines to compare the motion of each individual action from each view. For instance, elbow movement from the side view has been compared to elbow movement from the front view. (as opposed to the previous image that compared the actions relative to a view.)

Wii Tennis

A Wii Tennis match from the front and side spaning a duration of 5 seconds.

the fold in built form

UN Studio

One of the most difficult propositions of the “fold” is transition from abstraction to tangible. It is easy enough to read and understand Deleuze, Grosz, Lynn, and Vidler but overwhelmingly difficult to translate their concepts to built form. (Keep in mind that this is all relative, meaning, understanding them is not easy and hence translating from abstraction to tangible seems nearly impossible.)

The work of Ben van Berkle and Caroline Bos of UN Studio cleverly and clear actualizes these abstract ideas. Most directly they have taken the mobius strip and it’s 3-dimensional equivalent, the klien bottle, objects that literally have no inside or outside, and lack orientation or direction, and translated them into built form. They have used the mobius strip as the basis for their Mobius House to sponsor overlap and interaction between all aspects of living and working cycles.

UN Studio use the klein bottle as the conceptual frame work for their Living Tomorrow pavilion.

Finally the fold is most clearly illustrated by the Villa NM. Split-level programmatic functions of a house are mediated, separated, and connected by a fold.

repositioning the either/or with the both/and

In “Skin and Bones”, a chapter in Warped Space, Anthony Vidler is primarily concerned with exploring the space between, the liminal, and the relationship between inside and outside. He discusses the inbetween/liminal/inside/outside in the terms of the “fold” or pli. The fold is understood as both “a material phenomenon” (the actual) and “a metaphysical idea” (the virtual) that “joins the soul to the mind without division.” It is both a connector and separator, infinite and instant, and a threshold of the either/or. He positions this concept in terms of Leibinz’s idea of the fold and Deleuze’s interpretation of the Leibniz fold.

Deleuze’s understands the fold as both abstract and physical. Vidler translates, “folds exist in space and in time, in things and in ideas, and among their unique properties is the ability to join all these levels and categories at the same moment.” The fold puts the inside and outside in relation. Deleuze, in the final chapter of Foucault writes, “The outside is not a fixed limit but moving matter animated by peristaltic movements, folds and foldings that altogether make up an inside: they are not something other than the outside, but precisely the inside of an outside.” It is a moment of transition where all things exist and are mediated, joined both physically and conceptually.

Elizabeth Grosz, in Architecture from the Outside, extends (indirectly) the Deleuzian fold to encompass the real and virtual. Grosz structures the idea of the virtual, as opposed to the actual, as a way of relating and connecting past with present with future, and space with time. The interaction of the virtual with the actual allows overlaps and singularities of duration, memory, past, and present. It allows for simultaneity (a single point) and infinity to occur at the same time. “The past exists, but in a state of latency or virtuality . . . The present can be understood as . . . the point where the past intersects most directly with the body.” Virtuality relates the condition of the present within the scope of the past (and hence future) creating the body as the point of interaction with duration as a component of time.

Vidler takes these relationships of the inside/outside, virtual/actual, and past/present/future and extends them to architecture. He notes that some contemporary architects, such as Greg Lynn, are able to use digital media to realize the fold in both built and conceptual architecture. The results are new “blob,” “viscous,” and topological” forms. The inside is the outside. The new forms result from forces and motion that simultaneously respond to internal and external context. The fold can be the entire building or moments that mediate between separate pieces. It is a singular event existing in the present that disrupts and repositions our perception of architecture within time (past and future) and space.

The Easton + Combs Prehistory Museum

The Easton + Combs Prehistory Museum, Gyeonggi-do Jeongok, South Korea, is a good illustration of Lynn’s animate form. Easton + Combs simultaneously respond to the internal and external forces acting on the design and organization of the Prehistory Museum. The hexagonal nodes are result of the context, the archaeological site, and programmatic connections. The program is distributed in a series of exterior and interior nodes that each have a field of influence/attraction/force that actively relate to each other. The resulting form not only organizes program and conditions but also acts as a structural space frame.

Lynn, go back to math class

In Animate Form Lynn co-opts math terms to define new terms for discussing animation and digital process. He is generally right, but not in precise ways, and sometimes wrong. For instance, he defines a type of animate form as “topologically entities” and discusses the implications of “topological form.” There is no topological form. Topology is field of geometry that is concerned with determining when things are the same. Determining when two things are exactly the same is nearly impossible and not practical to study. In topology two things are considered the same when there exists a homeomorphic map between them. Simply (and not rigorously), this means that two things are the same when you can deform one into the other with out adding or taking away any holes. Lynn takes the term topology from this idea, using it to describe surface manipulation. Not quite right.

Lynn further describes the temporal component of topology as, “the immanent curvatures that result from the combinatorial logic of differential equations.” This makes absolutely no sense. Simply, combinatorics is a type of pure math concerned with counting. A differential equation is an equation or an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders. (wikipedia) One is a type of equation in calculus and one is a branch of pure math. While there are relationships between the two, I’m not convinced Lynn knows what he is actually saying. He is taking combinatorial to be synonymous with combination. I think he really means the immanent curvatures that result from the combination of differential equations.

Lynn needs to either describe (correctly) why and how he is using math terms or not use them at all.

“an environment of force and motion”

Greg Lynn’s Animate Form

In Animate Form, Greg Lynn carefully and comprehensively delineates a new(ish) field of design and process. To do he has defined new terms and issues for describing his thesis. He redefines (or clarifies) some terms and co-opts terms from math and science. The most important (re)definition is of animate/animation as not just the movement of objects but rather “impl[ing] the evolution of a form and its shaping forces.” Animate form is an environment of forces and motion as opposed to the more traditional way of thinking of design and form as static points. It is not necessarily literal motion, but is a range of forces acting on continuous surfaces/forms rather than a collection of points. There is no single definable point but rather fields of influence.

He argues that designing by manipulating the forces and areas of influence sponsors multiplicity of event/time/instant in a single form. This facilitates a greater response to a range of shifting and static contextual conditions than traditional design allows. For instance, site, program, and movement of people can all be conceived of as forces and motion simultaneously acting on and responding to form.

Lynn uses his newly minted terms and concepts to launch a fairly comprehensive attack on traditional processes and practices of design and architecture. “Architecture remains as the last refuge for members of the flat-earth society.” He points out that, “buildings are often assumed to have a particular and fixed relationship to their programs.” Buildings are rarely designed for a flexibility of program and never designed to sponsor an often inevitable shifting of use/program over the life span of a building. Lynn’s concept of the performance envelope models a range of programmatic/typological relationships and interaction potentials. Again the focus is on the multiplicity and mutability sponsored by an animate process.

Lynn makes a productive argument for the inclusion of digital media in the design process. Often the role of digital media and technology in architecture is questioned, its value being subjugated as merely a tool for representation, efficiency, and production. Designs generated from digital modeling have typically been little more than shallow, surface based forms that are justified post facto with flimsy pseudo intellectual reasoning. Additionally, “because of the stigma and fear of releasing control of the design process to software, few architects have attempted to use the computer as a schematic, organizing generative medium for design.” The use of new technology in architecture typically has an incubation period while architects figure out its range, capacity and limitations. We have to define digital process in its own terms rather than in terms from traditional design. For example, when steel was first introduced as a building material, architects designed forms that still mimicked traditional masonry construction. The full potential of steel was not realized until it was defined in its own terms.

Lynn gives us a linguistic and conceptual framework in which we can design and work using digital process and animate form.