project 2b - Constructed Morphology

The intent is to model a physical construct based on the analysis done in 2a (see previous post) that results in a surface. I used my diagram of the darjeeling limited to construct a form work for creating a surface.

construction documents:





the process:

project 2a_the darjeeling limited

"Model, animate and construct an image of the procedural sequence(s) by the director/cinematographer in constructing the space and time of the selected portion of the scene from your film."

selected scene from the darjeeling limited



The train provides a series of vertical and horizontal datums by which the camera moves and the characters vary. Here I have diagrammed the datums as lines, the main characters as black rectangles and the stewardess as a red rectangle.




Here is an composite of each frame diagram overlapped to exaggerate movement and relationships.

Versioning

Versioning encompasses a mode of thinking/designing/producing that made me say “duh, of course.” It’s one of those ideas that once stated seems obvious, you wonder why you didn’t think of it, and finally, why doesn’t everyone ‘version’.

While technology was a catalyst for versioning, versioning is not defined in terms of technology. As SHoP puts it “versioning implies the shifting of design away from a system of horizontal integration [designers as simply the generators of representational form] towards a system of vertical integration [designers driving how space is conceived and constructed and what its effects are culturally.] " Versioning is a non-linear, collaborative thinking/designing/producing process that integrates all the conventional aspects of design to build simultaneously. Essentially, each step actively influences and effects each other step, instead of a step 1, step 2, . . . step n = building process. As a result architects have to become the conductors of the entire process: design, development, engineering, construction, etc.

So where does technology factor into versioning? While not essential to versioning, new technology facilities the collaboration and integration of multiple disciplines simultaneously into the process in a way that has previously been impossible. Versioning shifts the profession from the ‘hero architect’ to a field where not only is authorship of a form or design indeterminable, it is no longer important. The role of the architect is no longer to pluck an already formed design from his or her mind, but rather to design and control the process by which the design and construction of architecture occur. As Ingeborg Rocker puts it, “the concept [or process] alters accordingly: formerly presumed to be an a priori transcendent essence or think-in-itself, the concept turns here into a creative in-forming act, an event that is intrinsically linked with the design’s literal information.” She continues, “the architect finds himself – as a designer – controlling a process rather than a design.”

Versioning, like most of the concepts and projects explored in our class, is inherently emergent. There is no intended end result, only a highly designed process that allows for unintended results. A recent example of versioning can be seen in Carl Lostritto’s thesis project. He wrote several scripts for skins that responded to contextual, programmatic, and formal parameters. There was not a priori results sought after, rather he designed the process (in this case scripting) by which the relevant parameters would vary and ultimately produce possible design solutions. Each script (there were four) was dependent on each other script, resulting in concurrent, non-linear design process. He designed a process (scripting) that responded to a set of parameters and lead to a set of possible solutions.

The real potential of versioning is its ability to allow us (architects) to take back the process of architecture. Currently we have developers on one end, contractors on another, the clients, engineers and computer programmers (etc., etc., etc.) boxing us in. We can’t let the narrow-minded goals of the developer, or the un-design educated computer programmer controlling the outcome of the design. We have to design the process, integrate multiple disciplines, and reinvent the role of the architect if we are to keep from becoming marginalized by other related professions.

project 1

1c

1c_sectioning

1b_animation

1b_frame

1b_combining the kit of parts

Here are some combination of the parts:


camera moving forward and normal focal length to wide focal length


camera moving backward and normal focal length to narrow focal length


camera moving backward and normal focal length to wide focal length

1b_the kit of parts

I have added a background to pick up shadows. Hopefully this will act to orient movement versus camera focal length change. Here are the elements of my kit of parts:


normal focal length to narrow focal length


normal focal length to wide focal length


camera translating forward along a path


camera translating backward along a path

rhythm/repetition_center/edge

The temporal construct consists of regularly spaced elements whose varying shape illustrates movement. In this animation I attempted to challenge the rhythm/repetition by animating the focal length of the camera. The construct does not move but the focal length starts wide (about 100 degrees) and ends narrow (about 40 degrees) compressing the apparent distance between the parts of the construct in relation to time. By leaving the construct at rest and animating I was attempting to emphasize that the “medium between the observer and the visible object as the reality of visual experience.” (Perez-Gomez)

The path and placement of the viewpoint was intended to subvert the reading of frame by putting the center/edge in motion. The viewpoint constantly shifts from one side, to the other side and from inside to outside causing the orientation of the frame to shift similarly.

Alberto Perez-Gomez and a brief history of geometry

Alberto Perez-Gomez and Louise Pelletier, in Architectural Representation and the Perspective Hinge, put in to question architects unwavering faith in the conventional set of projections (plan, section, elevation) that have been used to represent the idea of a building. He points out that they are symbols for a building not the actual building. “For architects it is important to remember that a symbol is neither a contrivance nor an invention—nor is it necessarily a representation of absolute truths or transcendental theological values.” It is clear that the conventional set of architectural projections is neither arbitrary nor a given.

This idea of an (un)stable foundation of conventional architectural representation can be put in relation when compared to the foundations of Euclidean Geometry. In Elements, thirteen books on geometry, Euclid defines an axiomatic system in which a finite set of axioms are take as true (without proof) and all theorems are proved from the initial set of axioms. We cannot prove anything with out accepting something as true or given. Euclid’s five axioms are:
1. Any two points can be joined by a straight line.
2. Any straight line segment can be extended indefinitely in a straight line.
3. Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
4. All right angles are congruent.
5. Parallel postulate. If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. (essentially, given a line M and a point P not on that line there exists only one line that goes through P and never intersects M.)

He also included 23 definitions such as point, line, and surface in addition to 5 “common notions,” which included, "things which equal the same thing are equal to one another,” and “if equals are added to equals then the sums are equal.” These are concepts that we have to accept as true if we are going to prove anything. Accepting these basic ideas and definitions as true, Euclid proved the theorems that appear in Elements and formed the basis for geometry for the next two thousand years.

Understand Euclidean geometry allows us to deconstruct conventional architectural representation. In architecture we have accepted projection and associated definitions as givens and proved our whole system of representation based on these assumptions. So what happens if we don’t accept the stated axioms as givens? In the early 19th century mathematicians began to question the parallel postulate. Could it be derived in terms of the other four axioms (and hence wasn’t an axiom but a theorem)? Were there theorems that had been derived that didn’t rely on the parallel postulate? It turns out that the first 28 theorems he proved are not derived based on the parallel postulate. This questioning of the fundamental axioms of geometry has led to new geometries. For instance, if we take the parallel postulate as false we get two new axioms, either 'there exists an infinite number of lines through P parallel to M' or 'there exists no lines through P parallel to M.' The former results in hyperbolic geometry and the latter in elliptic geometry.

So what happens if we don’t accept the basic foundation of conventional architectural representation as true? What if we think of them as false? What other systems of representation can be derived?

The most important idea to remember is that treating an underlying principal as false doesn’t necessarily give us the opposite of it. We get systems that are derived from various rule sets. For instance, Gothic architecture “operating though well-established traditions and geometric rules that could be applied directly on site,” was derived from an entirely different system of architectural representation than today. Conversely, contemporary architects are redefining rules within the conventional rule set. This still produces new systems of representation, but ones based on some of the same rules, similar to the Euclidean/Hyperbolic/Elliptic geometry relationship.

Lewis Tsurumaki Lewis has taken the generally accepted rule of ‘conventional architectural representations (plan, section, axon) need to remain separate to convey information’ and negated it, “conventional architectural representations need to be combined (ex. orthographically-projected-plan-sectioned-isometrics) to convey information.’ They have defined a new system based on the traditional conventions of representation and the redefinition of one of those rules. Additionally, SHoP architects have redefined architectural representation based on efficiency resulting in axonometric construction drawings and a general abandonment of orthographically projected architectural representation.

Now we are faced with the challenge of inventing new systems and conventions of architectural representation that are informative and appropriate to contemporary techniques and practices. Do we negate the traditional conventions and start over? Or do we return to older systems, such as the gothic tradition of building? The appropriate approach to rethinking the traditional system of architectural representation is to redefine specific axioms of convention that allow us to construct new systems out the fragments of tradition.

project 1a

relation and orientation

I've introduced a surface that traces the path of each wii mote movement which orients the path and structure of the construct. Here I have represented the paths as red:



I am uncertain if the red is necessary for the paths to be understandable. In the next video they are white. I've also extruded each vector surface to a point to try and map the conceptual center of the motion.




Here are some images investigating the use of red and surface vectors vs extruded mass vectors

Vector Field - The Very Many

In his January 15, 2007 entry The Very Many explores vector fields as an organizing system for the circulation and presentation areas of a gallery. He positions this project in terms of Greg Lynn, "from 'animate' rules, to shift in morphology, to mutate . . . "LE CHAMP"- has been the most litterally expressed via a field vectors, actual device support for presentation panels which should be simply laser-cut onto a full spectrum of colored acrylic panels."

animate wii

The camera is animated along the path of a spline curve generated from the points of the side vector diagram. The focal point of the camera is animated along the path of a spline curve generated from the points of the front vector diagram.

Here is an animation showing the path of the camera and focal point in relation to the construct.

temporal construct

Using the vector diagram of the front view and side view I’ve generated a new 3-demensional abstraction of the wii tennis movement. I rotated the front view vectors 90 degrees and then lofted corresponding vector from each view. This seems like a much better abstraction of wii tennis movement than previous attempts.

informative?

After more attempts at abstracting the wii mote in 3-dimensions I realized that I needed more information for it to be successful. I had only done a vector diagram of the wii mote motion taken from the front view. Here is the vector motion diagram of the side view. Hopefully this will allow me to generate more rigorous and informative 3-dimensional translations.

the hard part

Based on the various attempts at diagramming the motion associated with wii tennis, it’s clear that the vector diagrams of the wii mote force are the most interesting. That said, here is a first attempt at translating the vector wii mote into 3D. I took each vector and swept it along a spline curved generated from the end points of each vector. Interesting but not very informative. It seems like the force associated with each vector gets lost in this abstraction.

Interpreting Motion

Here are spline curves that are normal to the end of the wii mote. Control points are pulled in response to force of motion of each key frame. The top line is from the side view and the bottom line is from the front view. Trends and moments of stasis and motion are clearly evident.

To further respond to issues of force, I next used vectors that represent the force of the wii mote in each key frame.



This made me think of a vector field. This image is the composite overlay of the vectors of each key frame. (It’s not a vector field but resembles one).

Elbow/Wrist/Wii Mote

Here is a translation of the motion of my elbow, wrist, and wii mote into line diagram. The lines in the first image are generated by defining a point of each element (elbow/wrist/wii mote) in each key frame and then connecting them.

Here I've used a color to define the space between each element in the side and front camera views.

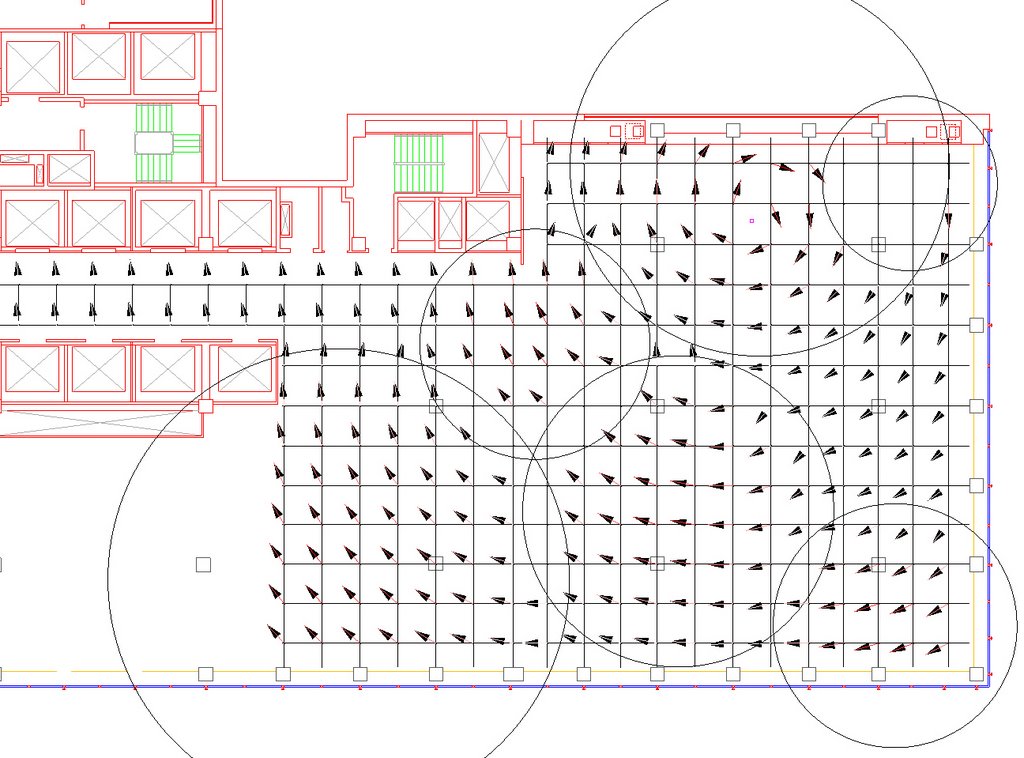
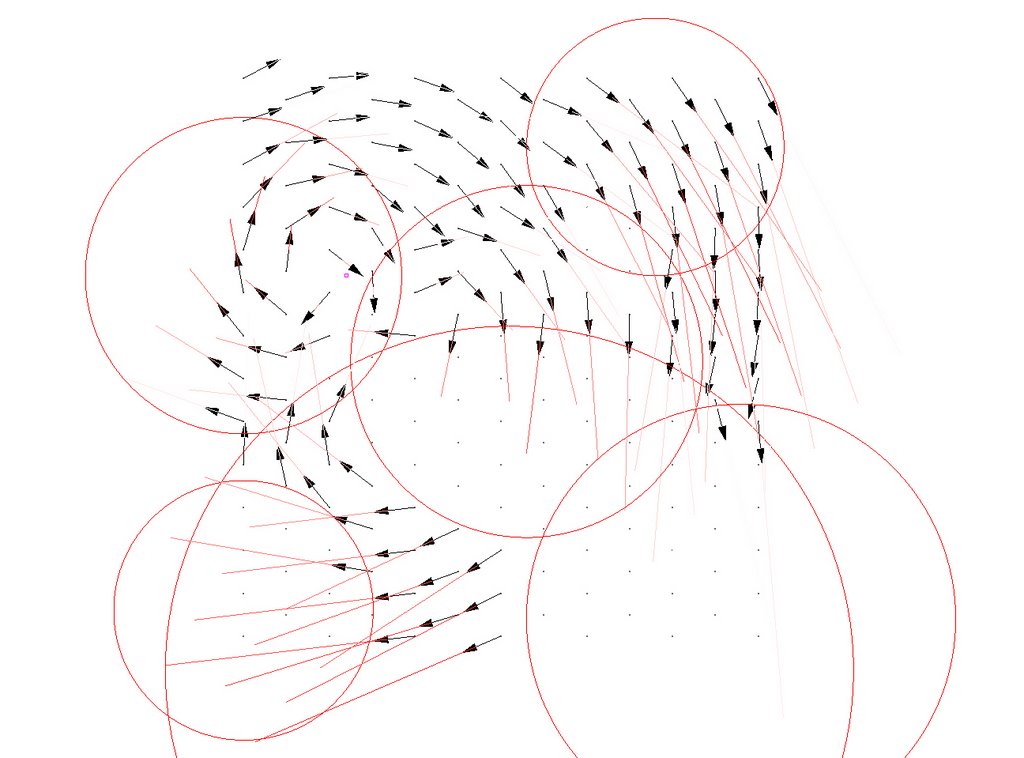
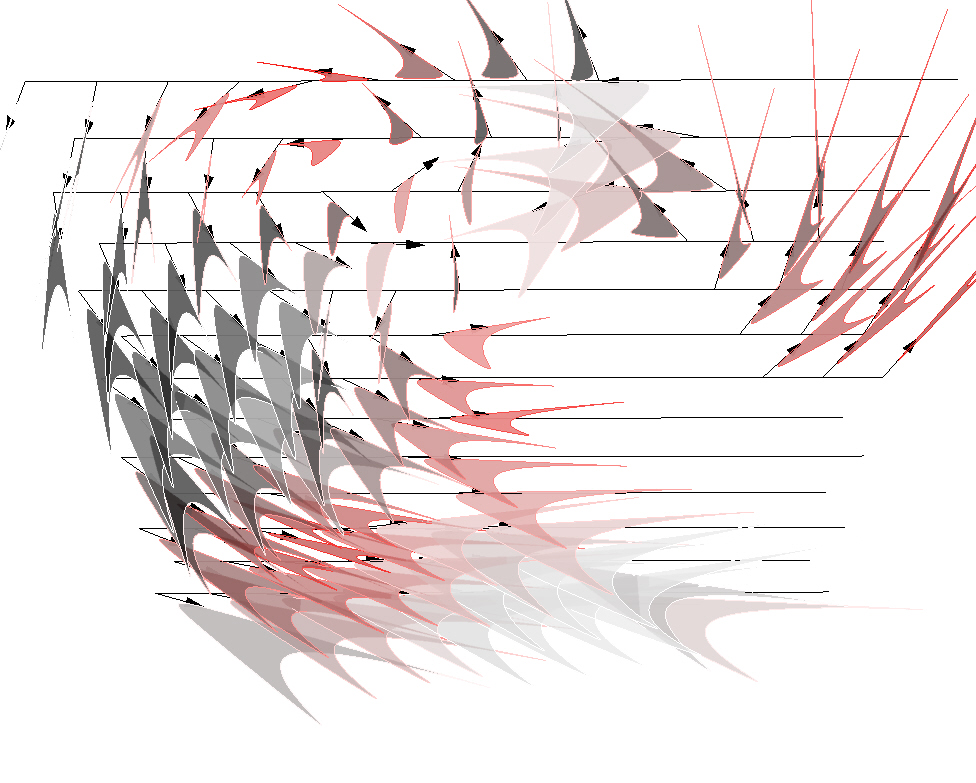
Here transitional lines between elbow/wrist/wii mote movement in the side and front views have been introduced. Variation in force are illustrated as well as changes in orientation.


Finally, I have used transitional lines to compare the motion of each individual action from each view. For instance, elbow movement from the side view has been compared to elbow movement from the front view. (as opposed to the previous image that compared the actions relative to a view.)

Wii Tennis

A Wii Tennis match from the front and side spaning a duration of 5 seconds.

the fold in built form

UN Studio

One of the most difficult propositions of the “fold” is transition from abstraction to tangible. It is easy enough to read and understand Deleuze, Grosz, Lynn, and Vidler but overwhelmingly difficult to translate their concepts to built form. (Keep in mind that this is all relative, meaning, understanding them is not easy and hence translating from abstraction to tangible seems nearly impossible.)

The work of Ben van Berkle and Caroline Bos of UN Studio cleverly and clear actualizes these abstract ideas. Most directly they have taken the mobius strip and it’s 3-dimensional equivalent, the klien bottle, objects that literally have no inside or outside, and lack orientation or direction, and translated them into built form. They have used the mobius strip as the basis for their Mobius House to sponsor overlap and interaction between all aspects of living and working cycles.

UN Studio use the klein bottle as the conceptual frame work for their Living Tomorrow pavilion.

Finally the fold is most clearly illustrated by the Villa NM. Split-level programmatic functions of a house are mediated, separated, and connected by a fold.